Abstract

We present a novel approach to path planning for robotic manipulators, in which paths are produced via iterative optimisation in the latent space of a generative model of robot poses. Constraints are incorporated through the use of constraint satisfaction classifiers operating on the same space. Optimisation leverages gradients through our learned models that provide a simple way to combine goal reaching objectives with constraint satisfaction, even in the presence of otherwise non-differentiable constraints. Our models are trained in a task-agnostic manner on randomly sampled robot poses. In baseline comparisons against a number of widely used planners, we achieve commensurate performance in terms of task success, planning time and path length, performing successful path planning with obstacle avoidance on a real 7-DoF robot arm.

Motivation

Path planning consists of finding a sequence of joint angles to move the robot from a start to a goal configuration. Traditional approaches suffer from a few issues. First, their planning time scales super-linearly as the complexity of the scene increases (as illustrated below). Optimisation-based planners are usually not flexible enough to handle constraints that cannot be directly expressed in joint space. Sampling-based planners, on the other hand, struggle to find solutions in scenarios where constraints render only a small volume of configuration space feasible.

One obstacle

Five obstacles

Overview

To address the previously mentioned issues, we introduce Latent Space Path Planning (LSPP). Our idea is to first learn a latent representation of valid robot states. We then learn high-level performance predictors acting on this latent space as well as environment information to guide optimisation in latent space. Performing this optimisation iteratively produces a sequence of latent values that translates to a joint-space path satisfying the constraints.

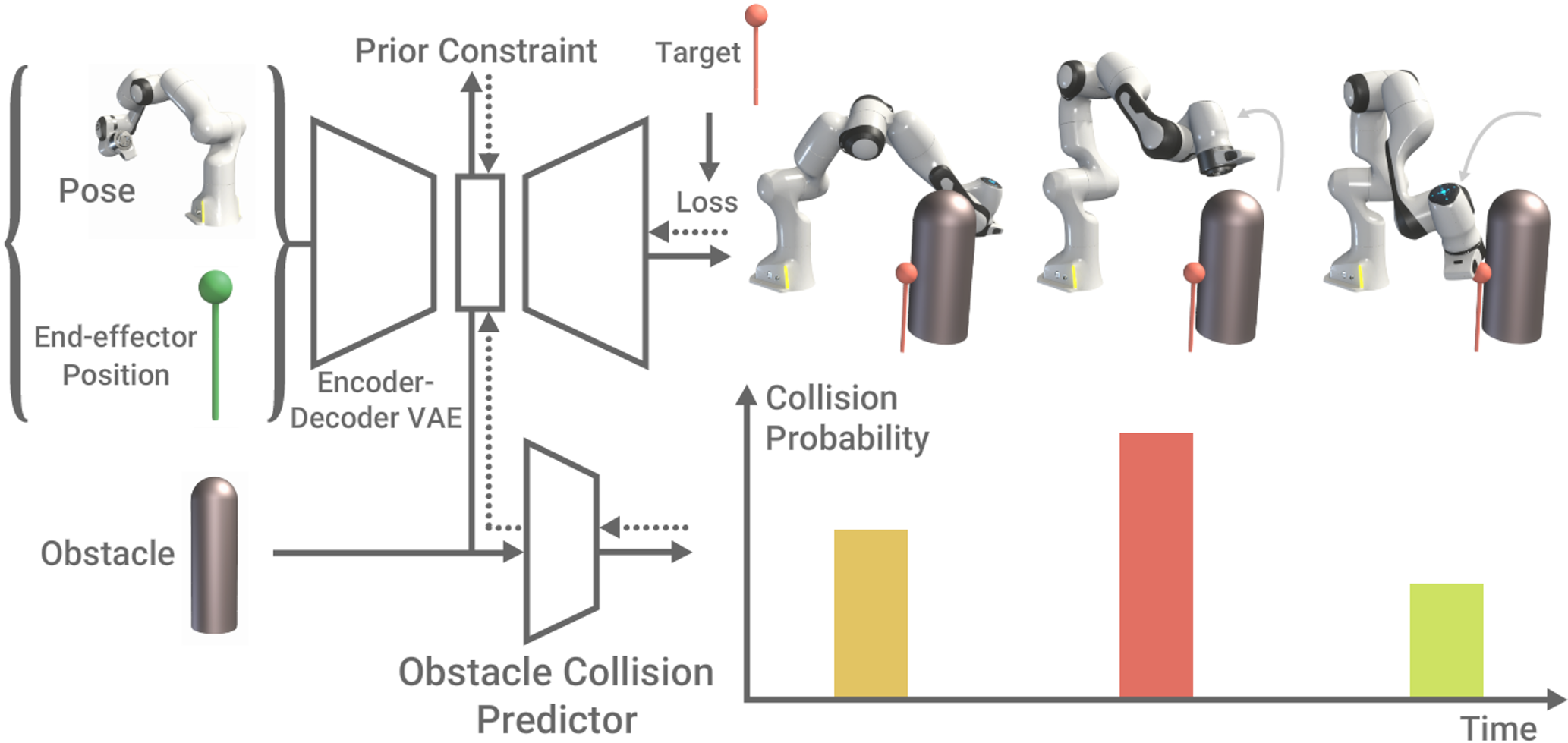
Approach

We learn a latent representation of robot state through a variational autoencoder (VAE). Our model takes as input a joint configuration and its corresponding end-effector position, encodes them to a latent state z and then decodes it back. Given a target position, the end-effector position of the VAE output is used to compute the distance to the target. Paths for target reaching are produced through the iterative use of activation maximisation (AM). In other words, we iteratively backpropagate the gradient of the target loss to the latent space. A planned path is produced by decoding a sequence of latent values and taking the joint configuration of the VAE output. Note that our approach does not assume access to the forward kinematics relationship. Thus, we did not take joint configuration of the VAE output to compute the target loss.

Without modification, AM may often drive the latent values into parts of the latent space that have not been seen during training. Decoding these latent representations can lead to poor (joint configuration, end-effector position) pairs that are inconsistent with the desired kinematics. To encourage the optimisation to traverse regions in which the model is well defined, we introduce an additional loss term to the AM objective consisting of the likelihood of the current latent representation under its prior.

Finally, to avoid obstacles, a collision classifier, taking as input the concatenation of latent value z and obstacle information o, is trained using a binary cross entropy loss while the VAE weights remain frozen. When performing AM in the case of obstacle avoidance, we add an obstacle loss term from binary cross entropy loss to the AM loss. Our approach handles multiple obstacles by simply taking the sum of individual obstacle losses.

Experimental results

Qualitatively, in the case of no prior loss, one of the joints reaches its joint limit and the robot fails to reach the target, whereas in the case of adding the prior loss, the robot successfully reaches the target.

No prior loss

Prior loss

The obstacle loss is critical in avoiding obstacles as demonstrated below. Without any obstacle loss, the robot ignores the obstacle and bumps into it directly. The neon light shows the colliders, and it turns red when it is in collision. Adding the obstacle loss guides the robot to reach the target while avoiding the obstacle.

No obstacle loss

Obstacle loss

Comparision against established path planning baselines from MoveIt

One obstacle

LSPP (ours)

RRTConnect

LBKPIECE

RRT*

LazyPRM*

FMT*

BIT*

CHOMP

Three obstacles

LSPP (ours)

RRTConnect

LBKPIECE

RRT*

LazyPRM*

FMT*

BIT*

CHOMP

Real-world experiment

Real-world panda

Top-down view

Citation

@article{hung2022reaching,
  title={Reaching Through Latent Space: From Joint Statistics to Path Planning in Manipulation},
  author={Hung, Chia-Man and Zhong, Shaohong and Goodwin, Walter and Jones, Oiwi Parker and Engelcke, Martin and Havoutis, Ioannis and Posner, Ingmar},
  journal={IEEE Robotics and Automation Letters},
  volume={7},
  number={2},
  pages={5334--5341},
  year={2022},
  publisher={IEEE}
}

Acknowledgement

This work was supported by the UKRI/EPSRC Programme Grant [EP/V000748/1], NIA [EP/S002383/1], the RAIN [EP/R026084/1] and ORCA [EP/R026173/1] Hubs, the Clarendon Fund and Amazon Web Services as part of the Human-Machine Collaboration Programme. The authors also gratefully acknowledge the use of the University of Oxford Advanced Research Computing (ARC) facility in carrying out this work (http://dx.doi.org/10.5281/zenodo.22558) and the use of Hartree Centre resources. We thank Jonathan Gammell for insightful feedback and discussions, and Rowan Border for helping with setting up BIT* and interfacing between OMPL and MoveIt. We also thank Yizhe Wu for recording real-world experiments, and Jack Collins for proofreading our work.